What
does it do? Support
vector machine (SVM) learns a hyper plane to classify data into 2
classes. At a high-level, SVM performs a similar task like C4.5
except SVM doesn’t use decision trees at all.
What
is hyper plane?
A hyper plane is a function like the equation for a line, y = mx +
b.
In fact, for a simple
classification task with just 2 features, the hyper plane can be a
line.
SVM
can perform a trick to project our data into higher dimensions. Once
projected into higher dimensions, SVM figures out the best hyper
plane which separates your data into the 2 classes.
Example:
The simplest example is bunch of positive samples and negative
samples on a table. If the samples are not too mixed together, we
could take a stick and without moving the balls, we can separate them
with the stick.
When
a new sample is added on the table, by knowing which side of the
stick the sample is on, we can predict whether the sample is positive
or negative. The
samples represent data points, and the positive and negative samples
represent 2 classes. The stick represents the hyper plane which in
this case is a line. SVM
figures out the function for the hyper plane.
So
there are so many possibilities of drawing hyper planes. Conceder the
following diagrams.
Figure
A,B and C are some examples for possible hyper planes that could be
drawn but we need to select the optimal hyper plane that could be
drawn. The hyper plane must be drawn in widest street manner that
separates the positive samples from negative samples hence it is
called widest
street approach.
Margins
are often associated with SVM. The margin is the distance between the
hyper plane and the 2 closest data points from each respective class.
In the sample and table example, the distance between the stick and
the closest positive and negative sample is the margin.
Margin
is also referred as widest street.
The
key is: SVM
attempts to maximize the margin, so that the hyper plane is just as
far away from positive sample as the negative sample. In this
way, it decreases the chance of misclassification.
Using
the positive sample, negative sample and table example, the hyper
plane is equidistant from a positive sample and a negative sample. These samples or
data points are called support vectors, because they support the
hyper plane. Hence the name Support
Vector Machine.
So
we have to make decision rule that would use that decision boundary
to find out whether sample will be placed in left side of the street
or right side of the street (STEP 1). Then we need to maximize the
margin in order to find out the optimal hyper plane (STEP 2). For
this
we
use a vector W̅ which is perpendicular to median line pq of the
street whose length is unknown yet.
STEP
1:
Let
‘U’ be a unknown and we need to find out whether U belongs to
right side of the street or left side of the street. We will draw a
vector U̅ as shown in the above figure.
W̅.
U̅ gives the projection of U̅ on W̅. So bigger the projection,
larger the tendency of sample being on positive or right side of the
street. This also implies that smaller the projection, larger the
tendency of sample being on negative or left side of the street. We
use a constant C in order to represent this relationship in
mathematical representation.
W̅.
U̅ ≥ C where C=-b
if
this condition satisfies then sample is on right side of the median
or may be positive or right side of the street. The same equation can
be represented as
W̅.
U̅+b ≥ 0
Decision
Rule
W̅.
U̅+b ≥ 0 if this condition satisfies then it implies that the
sample is positive otherwise the sample is negative.
The
problem with this is we don’t know what the value of W̅ or U̅ is.
W̅ must be perpendicular to median and there are various W̅ vectors
which are perpendicular to median and of various length.
If
we put enough constraints we are able to calculate W̅ and U̅.
Considering
the decision rule we have,
W̅.
X̟̅ + b ≥ 1 ----
Equation 1
If
this condition becomes true for a particular sample, then it implies
that sample will fall in right side of the street (or it is a
positive sample).
W̅.
X̠̅ + b ≤ -1
----
Equation 2
If
this condition becomes true for a particular sample, then it implies
that sample will fall in left side of the street (or it is a negative
sample).
For
mathematical convenience, we combine above two equation using a
variable ‘Yᵢ’.
Yᵢ
is +1 for positive samples
Yᵢ
is -1 for negative samples
Now
multiplying Yᵢ with the equations 1 and 2, we will get
[
W̅. X̟̅ + b ≥ 1 ] * Yᵢ ->
Yᵢ (W̅. X̅ᵢ + b) ≥ 1 where Yᵢ=+1 ->
Yᵢ (W̅. X̅ᵢ + b) -1 ≥ 0
[
W̅. X̠̅ + b ≤ -1 ] * Yᵢ -->
Yᵢ (W̅. X̅ᵢ + b) ≥ 1 where Yᵢ=-1 ->
Yᵢ (W̅. X̅ᵢ + b) -1 ≥ 0
Both
the equations are same, but the same expression may appear in two
forms depending on the sample. Either it may appear in the form
Yᵢ
(W̅. X̅ᵢ + b) -1 ≥ 0
This
implies that depending on the value of Yᵢ, the sample will fall in
either right side or left side of the street.
Or
Yᵢ
(W̅. X̅ᵢ + b) -1= 0
This
implies that the sample will fall inside the street or margin.
STEP
2:
SVM
attempts to maximize the margin, so that the hyper plane is just as
far away from positive sample as the blue negative sample. In this
way, it decreases the chance of misclassification.
Consider
the following diagram in order to find out the width of the street.
Consider
two vectors X̟̅ and X̠̅. And we know that W̅ is normal to
median. Hence
Width
of the street =
(X̟̅- X̠̅).
(W̅/|W|) where
W̅/|W| gives unit vector
We
know that Yᵢ (W̅.
X̅ᵢ + b) -1= 0 so
above equation will become
WIDTH
= (X̟̅-
X̠̅). (W̅/|W|)
=
(1-b+1+b) / |W|
=
2 / |W|
Hence
WIDTH = 2/ |W|
So
we need to maximize the width, That is, we need to maximize 2/ |W|.
This also implies that we need to minimize the value of |W|. The
effective way to minimize the value of |W| is taking half the value
of the square of the decision vector magnitude, i.e 0.5 * (|W|) ²
So
in order to minimize 0.5 * (|W|) ² or maximize the width of the
street we use Lagrange multiplier. Lagrange multiplier helps us to maximize or minimize particular function without thinking about the
constraint. We use a variable L in order to maximize the width of the
street. As Lagrange is used to maximize or minimize without
considering the constraints,
In
order to find out the decision vector value, differentiate the above
equation with respect to W̅,
This
implies that decision vector is sum of all sample vector.
Differentiate
the same equation with respect to b,
What
this maximisation expression depicts
-
Maximisation depends on the sample vectors.
-
And optimisation of this depends only on the dot product of pairs of samples.
Decision
vector also depends on dot product of sample vector and unknown
sample.
This
can be proved as,
If
the positive samples and negative samples are mixed together, a
straight line will not work. So in that scenario, quickly lift up the
table throwing the samples in the air. While the samples are in the
air and thrown up in just the right way, use a large sheet of paper
to divide the balls in the air. Lifting up the table is the
equivalent of mapping our data into higher dimensions. It can be
called as transformation. In this case, we go from the 2 dimensional
table surface to the 3 dimensional samples in the air.
By
using a kernel we have a nice way to operate in higher dimensions.
The large sheet of paper is still called a hyper plane, but it is now
a function for a plane rather than a line. SVM does its thing, maps
them into a higher dimension and then finds the hyper plane to
separate the classes.
Let’s
consider this new transformation as Φ(X̅).
But
we never used X̅ vector individually anywhere in the above process.
We always used it as a dot product of some other vector.
So
kernel provides a function in order to find out that dot product
using the following equation
K(X,Z)
= Φ(X̅) . Φ(Z̅)





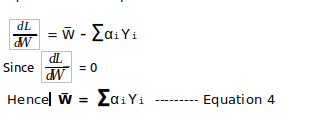


No comments:
Post a Comment